I. Introduction
Fractals are mathematical objects that exhibit self-similar properties at different scales. This means that when you zoom in/out on a fractal shape, each of its parts looks very similar to the whole; that is, similar geometric patterns or structures repeat at different magnification levels (see fractal examples in Figure 1). Most fractals have intricate, detailed, and infinitely complex shapes.
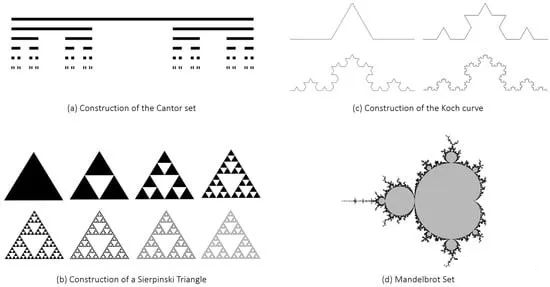
figure 1
The concept of fractals was introduced by mathematician Benoit B. Mandelbrot in the 1970s, although the origins of fractal geometry can be traced back to the earlier work of many mathematicians, such as Cantor (1870), von Koch (1904), Sierpinski (1915), Julia (1918), Fatou (1926), and Richardson (1953).
Benoit B. Mandelbrot studied the relationship between fractals and nature by introducing new types of fractals to simulate more complex structures, such as trees, mountains, and coastlines. He coined the word "fractal" from the Latin adjective "fractus", meaning "broken" or "fractured", i.e. composed of broken or irregular pieces, to describe irregular and fragmented geometric shapes that cannot be classified by traditional Euclidean geometry. In addition, he developed mathematical models and algorithms for generating and studying fractals, which led to the creation of the famous Mandelbrot set, which is probably the most famous and visually fascinating fractal shape with complex and infinitely repeating patterns (see Figure 1d).
Mandelbrot's work has not only had an impact on mathematics, but also has applications in various fields such as physics, computer graphics, biology, economics, and art. In fact, due to their ability to model and represent complex and self-similar structures, fractals have numerous innovative applications in various fields. For example, they have been widely used in the following application areas, which are just a few examples of their wide application:
1. Computer graphics and animation, generating realistic and visually attractive natural landscapes, trees, clouds, and textures;
2. Data compression technology to reduce the size of digital files;
3. Image and signal processing, extracting features from images, detecting patterns, and providing effective image compression and reconstruction methods;
4. Biology, describing the growth of plants and the organization of neurons in the brain;
5. Antenna theory and metamaterials, designing compact/multi-band antennas and innovative metasurfaces.
Currently, fractal geometry continues to find new and innovative uses in various scientific, artistic and technological disciplines.
In electromagnetic (EM) technology, fractal shapes are very useful for applications that require miniaturization, from antennas to metamaterials and frequency selective surfaces (FSS). Using fractal geometry in conventional antennas can increase their electrical length, thereby reducing the overall size of the resonant structure. In addition, the self-similar nature of fractal shapes makes them ideal for realizing multi-band or broadband resonant structures. The inherent miniaturization capabilities of fractals are particularly attractive for designing reflectarrays, phased array antennas, metamaterial absorbers and metasurfaces for various applications. In fact, using very small array elements can bring several advantages, such as reducing mutual coupling or being able to work with arrays with very small element spacing, thus ensuring good scanning performance and higher levels of angular stability.
For the reasons mentioned above, fractal antennas and metasurfaces represent two fascinating research areas in the field of electromagnetics that have attracted a lot of attention in recent years. Both concepts offer unique ways to manipulate and control electromagnetic waves, with a wide range of applications in wireless communications, radar systems and sensing. Their self-similar properties allow them to be small in size while maintaining excellent electromagnetic response. This compactness is particularly advantageous in space-constrained applications, such as mobile devices, RFID tags, and aerospace systems.
The use of fractal antennas and metasurfaces has the potential to significantly improve wireless communications, imaging, and radar systems, as they enable compact, high-performance devices with enhanced functionality. In addition, fractal geometry is increasingly being used in the design of microwave sensors for material diagnostics, due to its ability to operate in multiple frequency bands and its ability to be miniaturized. Ongoing research in these areas continues to explore new designs, materials, and fabrication techniques to realize their full potential.
This paper aims to review the research and application progress of fractal antennas and metasurfaces and compare existing fractal-based antennas and metasurfaces, highlighting their advantages and limitations. Finally, a comprehensive analysis of innovative reflectarrays and metamaterial units is presented, and the challenges and future developments of these electromagnetic structures are discussed.
2. Fractal Antenna Elements
The general concept of fractals can be used to design exotic antenna elements that provide better performance than conventional antennas. Fractal antenna elements may be compact in size and have multi-band and/or broadband capabilities.
The design of fractal antennas involves repeating specific geometric patterns at different scales within the antenna structure. This self-similar pattern allows us to increase the overall length of the antenna within a limited physical space. In addition, fractal radiators can achieve multiple bands because different parts of the antenna are similar to each other at different scales. Therefore, fractal antenna elements can be compact and multi-band, providing a wider frequency coverage than conventional antennas.
The concept of fractal antennas can be traced back to the late 1980s. In 1986, Kim and Jaggard demonstrated the application of fractal self-similarity in antenna array synthesis.
In 1988, physicist Nathan Cohen built the world's first fractal element antenna. He proposed that by incorporating self-similar geometry into the antenna structure, its performance and miniaturization capabilities could be improved. In 1995, Cohen co-founded Fractal Antenna Systems Inc., which began to provide the world’s first commercial fractal-based antenna solutions.
In the mid-1990s, Puente et al. demonstrated the multi-band capabilities of fractals using Sierpinski’s monopole and dipole.
Since the work of Cohen and Puente, the inherent advantages of fractal antennas have attracted great interest from researchers and engineers in the field of telecommunications, leading to further exploration and development of fractal antenna technology.
Today, fractal antennas are widely used in wireless communication systems, including mobile phones, Wi-Fi routers, and satellite communications. In fact, fractal antennas are small, multi-band, and highly efficient, making them suitable for a variety of wireless devices and networks.
The following figures show some fractal antennas based on well-known fractal shapes, which are just a few examples of the various configurations discussed in the literature.
Specifically, Figure 2a shows the Sierpinski monopole proposed in Puente, which is capable of providing multi-band operation. The Sierpinski triangle is formed by subtracting the central inverted triangle from the main triangle, as shown in Figure 1b and Figure 2a. This process leaves three equal triangles on the structure, each with a side length of half that of the starting triangle (see Figure 1b). The same subtraction procedure can be repeated for the remaining triangles. Therefore, each of its three main parts is exactly equal to the whole object, but in twice the proportion, and so on. Due to these special similarities, Sierpinski can provide multiple frequency bands because different parts of the antenna are similar to each other at different scales. As shown in Figure 2, the proposed Sierpinski monopole operates in 5 bands. It can be seen that each of the five sub-gaskets (circle structures) in Figure 2a is a scaled version of the whole structure, thus providing five different operating frequency bands, as shown in the input reflection coefficient in Figure 2b. The figure also shows the parameters related to each frequency band, including the frequency value fn (1 ≤ n ≤ 5) at the minimum value of the measured input return loss (Lr), the relative bandwidth (Bwidth), and the frequency ratio between two adjacent frequency bands (δ = fn +1/fn). Figure 2b shows that the bands of the Sierpinski monopoles are logarithmically periodically spaced by a factor of 2 (δ ≅ 2), which corresponds to the same scaling factor present in similar structures in fractal shape.
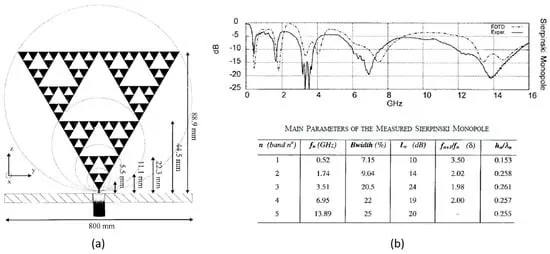
figure 2
Figure 3a shows a small long wire antenna based on the Koch fractal curve. This antenna is proposed to show how to exploit the space-filling properties of fractal shapes to design small antennas. In fact, reducing the size of antennas is the ultimate goal of a large number of applications, especially those involving mobile terminals. The Koch monopole is created using the fractal construction method shown in Figure 3a. The initial iteration K0 is a straight monopole. The next iteration K1 is obtained by applying a similarity transformation to K0, including scaling by one third and rotating by 0°, 60°, −60°, and 0°, respectively. This process is repeated iteratively to obtain the subsequent elements Ki (2 ≤ i ≤ 5). Figure 3a shows a five-iteration version of the Koch monopole (i.e., K5) with a height h equal to 6 cm, but the total length is given by the formula l = h ·(4/3) 5 = 25.3 cm. Five antennas corresponding to the first five iterations of the Koch curve have been realized (see Figure 3a). Both experiments and data show that the Koch fractal monopole can improve the performance of the traditional monopole (see Figure 3b). This suggests that it might be possible to "miniaturize" fractal antennas, allowing them to fit into smaller volumes while maintaining efficient performance.
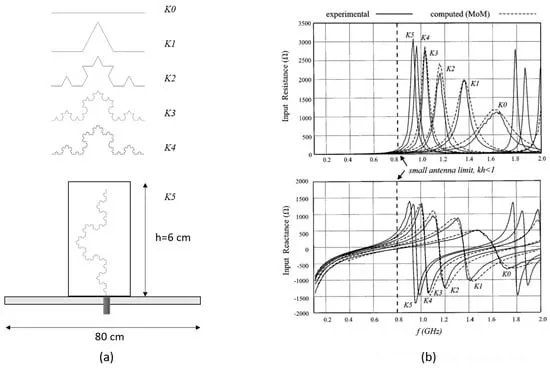
figure 3
Figure 4a shows a fractal antenna based on a Cantor set, which is used to design a wideband antenna for energy harvesting applications. The unique property of fractal antennas that introduce multiple adjacent resonances is exploited to provide a wider bandwidth than conventional antennas. As shown in Figure 1a, the design of the Cantor fractal set is very simple: the initial straight line is copied and divided into three equal segments, from which the center segment is removed; the same process is then iteratively applied to the newly generated segments. The fractal iteration steps are repeated until an antenna bandwidth (BW) of 0.8–2.2 GHz is achieved (i.e., 98% BW). Figure 4 shows a photograph of the realized antenna prototype (Figure 4a) and its input reflection coefficient (Figure 4b).
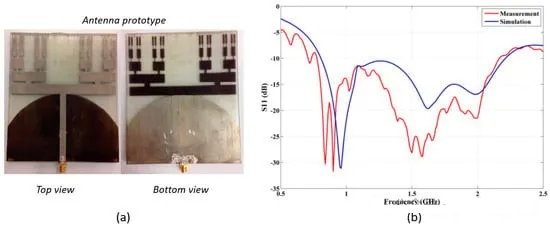
figure 4
Figure 5 gives more examples of fractal antennas, including a Hilbert curve-based monopole antenna, a Mandelbrot-based microstrip patch antenna, and a Koch island (or “snowflake”) fractal patch.
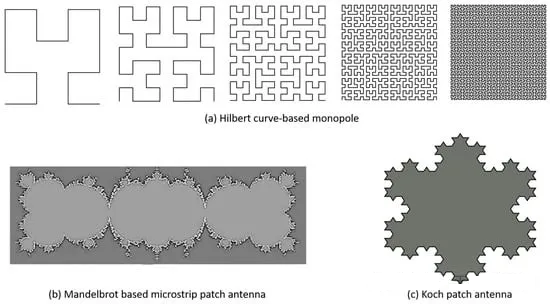
figure 5
Finally, Figure 6 shows different fractal arrangements of array elements, including Sierpinski carpet planar arrays, Cantor ring arrays, Cantor linear arrays, and fractal trees. These arrangements are useful for generating sparse arrays and/or achieving multi-band performance.
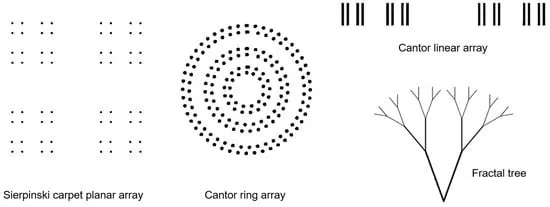
figure 6
To learn more about antennas, please visit:
Post time: Jul-26-2024







